Momento Cinético del Cuerpo Rígido
El momento angular es una magnitud física importante porque en muchos sistemas físicos constituye una magnitud conservada, a la cual bajo ciertas condiciones sobre las fuerzas es posible asociarle una ley de conservación. El hecho de que el momento angular sea bajo ciertas circunstancias una magnitud cuyo valor permanece constante puede ser aprovechado en la resolución de las ecuaciones de movimiento. En un instante dado, y fijado un punto del espacio en un punto del espacio O, se define el momento angular LO de un sistema de partículas respecto a ese punto como la integral siguiente:
Donde V, ρ(r) son el volumen del sólido y la densidad másica en cada punto, y Vo, ro son la velocidad de una partícula del cuerpo y el vector de posición respecto a O. Conviene recordar que el valor de la magnitud anterior depende de qué punto O se elija. Para el estudio de sólidos rígidos en movimiento conviene escoger un "punto móvil" (es decir, para cada instante del tiempo consideraremos un punto diferente del espacio). Por ejemplo podemos evaluar el momento angular respecto al centro de masas G del sólido:
Donde se ha introducido la abreviación r = rG.
Las partículas de un sólido rígido en rotación alrededor de un eje fijo describen circunferencias centradas en el eje de rotación con una velocidad que es proporcional al radio de la circunferencia que describen vi = ωr
 En la figura se muestra el vector momento angular Li de una partícula de masa mi cuya posición está dada por el vector ri y que describe una circunferencia de radio Ri con velocidad vi. El módulo del vector momento angular vale Li=rimivi Su proyección sobre el eje de rotación Z vale:
En la figura se muestra el vector momento angular Li de una partícula de masa mi cuya posición está dada por el vector ri y que describe una circunferencia de radio Ri con velocidad vi. El módulo del vector momento angular vale Li=rimivi Su proyección sobre el eje de rotación Z vale: Liz=ricos(90-q i)mivi, es decir,
El momento angular de todas las partículas del sólido es:
La proyección Lz del vector momento angular a lo largo del eje de rotación es:
El término entre paréntesis se denomina momento de inercia:
En general, el vector momento angular L no tiene la dirección del eje de rotación, es decir, el vector momento angular no coincide con su proyección Lz a lo largo del eje de rotación. Cuando coinciden se dice que el eje de rotación es un eje principal de inercia. Para estos ejes podemos relacionar el momento angular y la velocidad angular, dos vectores que tienen la misma dirección, la del eje de rotación |
El momento de inercia no es una cantidad característica como puede ser la masa o el volumen, sino que su valor depende de la posición del eje de rotación. El momento de inercia es mínimo cuando el eje de rotación pasa por el centro de masa.
Teorema del Momento Cinético
La derivada respecto al tiempo del momento angular de un sistema que se mueve en relación a un punto material es igual al momento, respecto a dicho punto, de las fuerzas exteriores que actúan sobre el sistema.
Es decir:
Mext=δL/δt. pues:
δL/δt = [(δr/δt) x (mv)] + [r x (δmv/δt)] = [v x (mv) + (r x F)] = 0 + r x F = M.
El teorema del momento cinético, establece que bajo condiciones similares al anterior teorema vectorial la suma de momentos de fuerza respecto a un eje es igual a la variación temporal del momento angular.
Derivando el momento cinético respecto al tiempo
El producto ma es la resultante de las fuerzas que actúan sobre la partícula, por tanto
Por tanto, la derivada respecto al tiempo del momento cinético respecto a un punto es igual al momento, respecto al mismo punto, de la fuerza neta que actúa sobre dicha partícula. Esto ocurrirá cuando la fuerza sea nula o cuando sea paralela al vector de posición (fuerza central). Por ello, podemos enunciar el teorema de conservación en la forma:
Si la fuerza neta que actúa sobre una partícula P es nula o es central con centro en un punto fijo O durante un cierto intervalo de tiempo, el momento cinético de la partícula respecto al punto O se mantiene constante durante dicho intervalo.
Caso de una Fuerza Nula
Si F = 0 el momento de la fuerza es naturalmente nulo y el momento angular es constante.
Podemos demostrar su constancia explícitamente. En ausencia de fuerza neta, una partícula sigue un movimiento rectilíneo y uniforme
Hallando el momento angular en cada instante
Ya que el producto vectorial de V0 por sí mismo se anula. La última cantidad ya no depende del tiempo, sino que es el valor inicial del momento cinético y por tanto éste es constante. El módulo de este momento cinético es
Siendo b el llamado parámetro de impacto: la mínima distancia del origen O a la que pasa la trayectoria rectilínea.
Caso de una Fuerza Central
Si la fuerza es todo momento paralela al vector de posición respecto al punto O, el producto vectorial r×F es nulo y el momento cinético respecto al punto O es constante
Obsérvese que esta conservación sólo se aplica al momento cinético calculado respecto al centro de fuerzas. Para cualquier otro punto, el momento cinético no será constante.
Primer Teorema de Koeing
El primer teorema de König proporciona una relación entre el valor del momento angular medida en un sistema inercial y que mide en el centro de masa. Afirma que el momento angular del sistema se puede escribir en el sistema inercial, como la suma del momento angular debido al movimiento del centro de masa CM y L del sistema para el centro de masa.
Este teorema es muy importante porque demuestra que el movimiento de un sistema de partículas, puede ser descompuesto en dos movimientos:
1. Un movimiento medio, es decir, el movimiento del centro de masa.
2. Un movimiento interno, es decir, el movimiento del sistema de puntos para el centro de masa.
Demostración
Supongamos por simplicidad como un polo del origen de sistema de referencia inercial : el momento angular está dada por
Supongamos por simplicidad como un polo del origen de sistema de referencia inercial : el momento angular está dada por
Se obtiene mediante el desarrollo de
Examinando con detalle las cuatro sumas nos damos cuenta de que el primer término representa el momento angular del centro de masa, el término segundo y tercero son cero, mientras que la cuarta y última es el momento angular respecto al origen del sistema inercia de una partícula con masa igual a la totalidad del sistema, coincidiendo con el centro de masa y la velocidad de la misma.
Ecuaciones Generales del Movimiento del Cuerpo Rígido.
Centro de Gravedad
El centro de gravedad o centro de masas de un sistema continuo es el punto geométrico definido como:
En mecánica del sólido rígido, el centro de masa se usa porque tomando un sistema de coordenadas centrado en él, la energía cinética total K puede expresarse como k = ½ MV2 + Krot, siendo M la masa total del cuerpo, V la velocidad de traslación del centro de masas y Krot la energía de rotación del cuerpo, expresable en términos de la velocidad angular y el tensor de inercia.
Velocidad Angular.
Sea una partícula cualquiera de un sólido rígido el cual se desplaza girando. Dado que todos los puntos están rígidamente conectados podemos hacer la siguiente descomposición de posición y velocidades, tomando un punto de referencia arbitrario
Donde
- r es vector posición del punto o partícula
- rc es la posición de un punto de referencia del sólido
- A(t)∈ SO(3)
- es la orientación, que viene dada por una matriz ortogonal
- R es la posición de la partícula con respecto al punto de referencia del cuerpo a lo largo del tiempo con una orientación variable.
- la R0 es la posición de partícula con respecto al punto de referencia del cuerpo en la orientación de referencia inicial.
- ω es la velocidad angular
- V es la velocidad total de la partícula
- Vc Es la velocidad "traslacional" o velocidad del punto de referencia.
Ecuaciones de Euler
Cuando las ecuaciones del movimiento de un sólido rígido se expresan en un sistema de referencia no inercial solidario con los ejes principales de inercia del sólido rígido toman una fórmula particularmente simple conocida como ecuaciones de Euler. En general, en este sistema de referencia es mucho más sencillo integrar las ecuaciones de movimientos que en un sistema de referencia inercial y no solidario con el cuerpo. Las ecuaciones de Euler para el movimiento de un sólido rígido tienen la forma:
Donde Mk son las componentes vectoriales del momento o torque total aplicado, IK son los momentos principales de inercia y ωk son las componentes del vector velocidad angular ω según los ejes principales de inercia.
Trabajo y Energía en el Movimiento del Cuerpo Rígido
En mecánica clásica, la energía cinética de un objeto puntual (un cuerpo tan pequeño que su dimensión puede ser ignorada), o en un sólido rígido que no rote, está dada en la ecuación Ec = ½ mv2 donde m es la masa y v es la rapidez (o velocidad) del cuerpo.
En mecánica clásica la energía cinética se puede calcular a partir de la ecuación del trabajo y la expresión de una fuerza F dada por la segunda ley de Newton:
La energía cinética se incrementa con el cuadrado de la rapidez. Así la energía cinética es una medida dependiente del sistema de referencia. La energía cinética de un objeto está también relacionada con su momento lineal:
Energía Cinética de un Sólido Rígido en Rotación
Para un sólido rígido que está rotando puede descomponerse la energía cinética total como dos sumas: la energía cinética de traslación (que es la asociada al desplazamiento del centro de masa del cuerpo a través del espacio) y la energía cinética de rotación (que es la asociada al movimiento de rotación con cierta velocidad angular). La expresión matemática para la energía cinética es:
Donde:
- Etra Energía de traslación.
- Erot Energía de rotación.
- mMasa del cuerpo.
I Tensor de (momentos de) inercia.
- ω =Velocidad angular del cuerpo.
- ω = Traspuesta del vector de la velocidad angular del cuerpo.
- v = Velocidad lineal del cuerpo.
El valor de la energía cinética es positivo, y depende del sistema de referencia que se considere al determinar el valor (módulo) de la velocidad v y ω. La expresión anterior puede deducirse de la expresión general:
En la Hidrodinámica cambia con mucha frecuencia la energía cinética por la densidad de la energía cinética. Esto se escribe generalmente a través de una pequeña e o una ε, así:
donde ρ describe la densidad del fluido.
Entendemos por energía cinética del sólido rígido la suma de las energía cinéticas del todas las partículas que lo constituyen. Como ya sabemos, la energía cinética es una magnitud física escalar relativa al observador en el referencial fijo XYZ.
Quedó demostrado que el movimiento más general del sólido rígido puede reducirse a una rotación de velocidad angular w con respecto a un eje que pasa por un punto arbitrario o, más una traslación cuya velocidad vo es la correspondiente a dicho punto. Así, la velocidad, en el referencial fijo, de un punto genérico Pi del sólido viene dada por:
Donde ri = oPi es el vector de posición del punto genérico Pi respecto del punto arbitrario o perteneciente al sólido. Si consideramos una partícula genérica de las que constituyen el cuerpo, digamos la partícula i-ésima, su energía cinética en el referencial fijo XYZ es
De modo que la energía cinética total del cuerpo Ek, teniendo en cuenta la relación, es:
y puesto que ni vo ni ω son propias de la partícula i-ésima, podemos escribir:
Segundo Teorema de Koening.
Donde m es la masa del cuerpo. Esta es la expresión general de la energía cinética del sólido rígido y es válida cualquiera que sea el punto o perteneciente al sólido con respecto al cual se mide ri.
Energía Cinética Rototranslatoria.
Debemos entender que la energía cinética de rotación es implemente la suma de las energías cinéticas de traslación ordinarias de todas las partículas del cuerpo referidas al centro de masa del mismo, y no una "nueva clase de energía". Esto se pone bien en evidencia si tenemos en cuenta que v′i = vi - vcm = ω × ri es la velocidad de la partícula i-ésima del cuerpo con respecto al centro de masa de éste, de modo que:
Así pues, la energía cinética de rotación es solamente una forma conveniente de designar una parte de la energía cinética del sólido rígido (energía cinética interna).
Traslación Pura
El cuerpo rígido puede tener un movimiento de traslación pura; en este tipo de movimiento, las velocidades de cada una de las partículas que componen al sólido, en cada instante de tiempo, son iguales (tener presente que la velocidad es un vector; esto implica que el módulo, la dirección y el sentido de la velocidad son iguales para todas las partículas en un instante dado). En general, el movimiento del sólido será curvilíneo y, por lo tanto, tendrá componentes de aceleración tangencial y normal.
Rotación Pura.
Si el único movimiento del cuerpo rígido es de rotación alrededor de un eje, decimos que el movimiento es de rotación pura; en este caso, las trayectorias de todas las partículas del sólido son circunferencias concéntricas; la velocidad de cada partícula tendrá la dirección y sentido del versor tangente a la circunferencia en cada instante de tiempo.
Asimismo, las velocidades de las distintas partículas que integran el sólido no serán las mismas; la única velocidad común será la velocidad angular del cuerpo.
Segundo Teorema de Koening.
El segundo teorema de König ( 1751 ) pertenece a la mecánica racional y afirma que la energía cinética total de un sistema de un sistema de referencia determinado (O, x1, x2, x3) es la suma de:
La energía cinética de traslación del centro "de masa" (que tienen una masa corporal igual al total del sistema con la velocidad de su centro de masa).
La energía cinética en comparación con una fuente de referencia en el centro de gravedad e invariable con respecto al eje de referencia (O, x1, x2, x3) .
Este teorema tiene muchas aplicaciones en la física , ya que hace posible el uso de algunos métodos desarrollados para el punto material con cuerpos extendidos.
Considere el sistema como un conjunto de N partículas, cada uno con masa m i y velocidad v en el sistema de referencia inercial. La energía cinética total del sistema muestra:
Sustituyendo v i = v 1 + v C H, donde v es la velocidad de una partícula en el marco de referencia del centro de masa y v C M es la velocidad del centro de masa en el sistema inercial, es:


















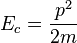









No hay comentarios:
Publicar un comentario