Antes de Estudiar los Conceptos Fundamentales de la Mecánica, Debemos Saber Cuál es el Significado de Ésta.
Mecánica.
Se puede definir como la ciencia que describe y predice las condiciones de reposo o movimiento de los cuerpos bajo la acción de fuerzas. Esta es una ciencia física puesto que estudia fenómenos físicos.
Sin embargo, algunos la asocian con las matemáticas, mientras que otros la consideran un tema de ingeniería. Ambos puntos de vista se consideran parcialmente, ya que la mecánica es la base de las mayorías de las ciencias de la ingeniería y es un requisito indispensable para estudiarlas.
Sin embargo no tiene el carácter empírico propio de algunas ciencias de la ingeniería, es decir, no se basa solo en la experiencia u observación, por su rigor y la importancia queda al razonamiento deductivo se parece a las matemáticas. Pero tampoco es una ciencia abstracta, ni siquiera una ciencia pura: es una ciencia aplicada. Su propósito es explicar y predecir los fenómenos físicos y poner las bases para aplicarlas en ingeniería.
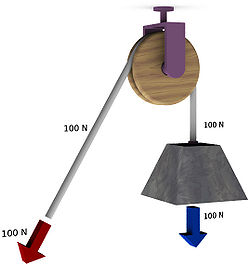 |
| La Mecánica comprende el estudio de las máquinas. |
Espacio.
Está asociado con la noción de la posición de un punto p. la posición de p puede ser definida por tres medidas de longitud a partir de cierto punto de referencia u origen, en tres direcciones dada. Estas longitudes se conocen como las coordenadas de p.
Tiempo.
Es considerad o como el intervalo de duración de un fenómeno.
Fuerza.
Esta representa la acción de un cuerpo sobre otro y puede ejercerse por contacto real o distancia, como en el caso de las fuerzas gravitacionales y magnéticas. Una fuerza se caracteriza por su o punto de aplicación, magnitud, dirección y se representa mediante un vector.
Masa.
Tiene la función de caracterizar y comparar los cuerpos con bases en ciertos experimentos mecánicos fundamentales. Por ejemplo tenemos: dos cuerpos que tengan la misma masa serán atraídos por la tierra de igual forma; también presentaran la misma resistencia a un cambio en su movimiento trasnacional.
El Factor de Conversión o de Unidad .
Es una fracción en la que el numerador y el denominador son medidas iguales expresadas en unidades distintas, de tal manera, que esta fracción vale la unidad. Método efectivo para cambio de unidades y resolución de ejercicios sencillos dejando de utilizar la regla de tres.
Un factor de conversión es una operación matemática, para hacer cambios de unidades de la misma magnitud, o para calcular la equivalencia entre los múltiplos y submúltiplos de una determinada unidad de medida.
- Ejemplo 1: pasar 15 pulgadas a centímetros (factor de conversión: 1 pulgada = 2,54 cm)
- 15 pulgadas × (2,54 cm / 1 pulgada) = 15 × 2,54 cm = 38,1 cm
- Ejemplo 2: pasar 25 metros por segundo a kilómetros por hora (factores de conversión: 1 kilómetro = 1000 metros, 1 hora = 3600 segundos)
- 25 m/s × (1 km / 1000 m ) : (3600 s / 1 h) = 90 km/h
- Ejemplo 3: obtener la masa de 10 litros de mercurio (densidad del mercurio: 13,6 kilogramos por decímetro cúbico) Nótese que un litro es lo mismo que un decímetro cúbico.
- 10 litros de mercurio × (1 decímetro cúbico de mercurio / 1 litro de mercurio) × (13,6 kilogramos / 1 decímetro cúbico de mercurio) = 136 kg
Análisis Dimensional.
Es una potente herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema de Vaschy-Buckingham (más conocido por teorema Π) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
- Analizar con mayor facilidad el sistema objeto de estudio
- Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.
El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números adimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real.
Finalmente, el análisis dimensional también es una herramienta útil para detectar errores en los cálculos científicos e ingenieriles. Con este fin se comprueba la congruencia de las unidades empleadas en los cálculos, prestando especial atención a las unidades de los resultados.
Procedimiento para el Análisis Dimensional.
Para reducir un problema dimensional a otro adimensional con menos parámetros, se siguen los siguientes pasos generales:
- Contar el número de variables dimensionales n.
- Contar el número de unidades básicas (longitud, tiempo, masa, temperatura, etc.) m
- Determinar el número de grupos adimensionales. El número de grupos o números adimensionales es n - m.
- Hacer que cada número dependa de n - m variables fijas y que cada uno dependa además de una de las n - m variables restantes (se recomienda que las variables fijas sean una del fluido o medio, una geométrica y otra cinemática; ello para asegurar que los números adimensionales hallados tengan en cuenta todos los datos del problema).
- Cada se pone como un producto de las variables que lo determinan elevadas cada una a una potencia desconocida. Para garantizar adimensionalidad deben hallarse todos los valores de los exponentes tal que se cancelen todas las dimensiones implicadas.
- El número que contenga la variable que se desea determinar se pone como función de los demás números adimensionales.
- En caso de trabajar con un modelo a escala, éste debe tener todos sus números adimensionales iguales a las del prototipo para asegurar similitud.
Ejercicio Resuelto.
Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad v dependerá de la altura h y de la gravedad g. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa m. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.
- Identificar las magnitudes de las variables:
- Formar la matriz
- Hacer el producto de matrices:
Aquí tenemos que decir que ϵk se refiere al exponente de la unidad k , pero éso se verá en pasos sucesivos.
- Desarrollar el producto de matrices y resolver el sistema de ecuaciones.
Se forma un sistema de ecuaciones. Si nos fijamos, tenemos 4 incógnitas, y sólo 3 ecuaciones, así que para que el sistema pueda ser resuelto, necesitamos tantas incógnitas como ecuaciones. ¿Cómo se subsana el problema? Muy sencillo: se coge un ϵk cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar ϵv como 1.
Si aplicamos la solución inicial que hemos propuesto anteriormente (ϵv=1), se realizan los sencillos cálculos y llegamos a las soluciones:
- Formar el/los grupos Π
Un grupo Π es una ecuación adimensional. ¿Cuántos grupos Π vamos a obtener? Pues si m es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y h el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos Π (o ecuaciones que obtendremos) será m - h. En el caso que nos ocupa, 4 - 3 = 1 ecuación.
Ahora se cogen las unidades que hemos tomado en nuestro problema y las elevamos a los exponentes que hemos obtenido. Ésa es nuestra ecuación.
(Nótese que Π es adimensional). Aquí obtenemos aquéllo que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.
Paso final: obtención de la ecuación.
v=k√(gh), con k valiendo 4 , lo que nos da la fórmula correcta: v=√(2gh)
Principales Unidades del Sistema Internacional en la Mecánica.
|
Velocidad | Metro por segundo | M/S | M/s |
| Velocidad angular | radian por segundo | | Rad/s |
| Volumen | | | |
| Sólidos | Metro cúbico | M³ | M³ |
| Líquidos | Litro | L | 10-1. m³ |
Equivalencias de las Unidades
Longitud:
| 1 milla | 1,6093 m. |
| 1 yarda | 0,9144 m |
| 1 pie | 0,3048 m. |
| 1 pulgada | 0,0254 m. |
| 1 milímetro | 0,0394 pulgadas ( ’ ). |
| 1centimetro | 0,3937 pulgadas ( ’ ). |
| 1 metro | 1,0936 yardas. |
| 1 kilómetro | 0,6214 millas. |
Superficie:
|
Derivadas.
Fuerza, área, densidad, velocidad, volumen, aceleración entre otras.
División de la Mecánica.
La mecánica de los cuerpos rígidos se subdivide en estática y dinámica:
- Estática. Trata sobre los cuerpos en reposo.
- Dinámica. Trata sobre los cuerpos en movimiento.
Ley de Homogeneidad.
Se dice que una ecuación es dimensionalmente homogénea cuando su forma no depende de las unidades de medidas, por ejemplo la ecuación que describe el recorrido de un cuerpo en caída libre que se suelta de reposo es, h=(g.t2)/2, donde h es la distancia recorrida, t es el tiempo transcurrido desde que se soltó y g es la aceleración de la gravedad, esta ecuación es validad tanto si la longitud se mide en pies, metros o pulgadas y el tiempo en horas, años o segundos, siempre y cuando g se mida en las mismas unidades de longitud y tiempo q h y t.
Ejercicios Resueltos:
1.- ¿Qué distancia recorrerá un automóvil en 6 horas, sabiendo que en 4 horas recorre 348 Kms. a velocidad constante?
Solución.
2.- Un depósito cilíndrico contiene 260 litros de agua cuando el nivel del líquido asciende a 30 cm. de altura. Al llegar el nivel del agua a 25 cm. de altura, ¿qué cantidad de agua contendrá aproximadamente el depósito cilíndrico?
Solución.
3- La distancia que hay del home al jardín central de un campo de beisbol es de 400 pies (ft), convierta esta cantidad a metros.
Solución:
4.- Convierta una longitud de 1500 millas a kilómetros.













No hay comentarios:
Publicar un comentario