Antes de empezar a estudiar el comportamiento de los cuerpos rígidos, es importante recordar que es un cuerpo rígido y los elementos que influyen en él.
Cuerpo Rígido.
Un cuerpo rígido puede ser considerado como un conjunto formado por un gran número de partículas que permanecen separadas entre sí por una distancia fija antes y después de aplicar la carga. Como resultado, las propiedades del material de que está hecho cualquier cuerpo que se suponga rígido no se tendrá que considerar cuando se analicen las fuerzas que actúan sobre éste. Cantidades Básicas: Las cuatro cantidades siguientes se utilizan en el equilibrio:
- Longitud: La longitud es necesaria para ubicar un punto en el espacio y de esta forma describir el tamaño de un sistema físico. Una vez que se define una unidad estándar de longitud, puede definirse cuantitativamente distancias y propiedades geométricas de un cuerpo como múltiplos de esa unidad de longitud.
- Tiempo: El tiempo se concibe como una sucesión de eventos. Aunque los principios de la Estática son independientes del tiempo, esta cantidad definitivamente juega un papel importante en el estudio de la Dinámica.
- Masa: La masa es una propiedad de la materia por la cual podemos comparar la acción de un cuerpo con la de otro.
Ángulos de Euler.
Los ángulos de Euler constituyen un conjunto de tres coordenadas angulares que sirven para especificar la orientación de un sistema de referencia de ejes ortogonales, normalmente móvil, respecto a otro sistema de referencia de ejes ortogonales normalmente fijos.
Fueron introducidos por Leonhard Euler en mecánica del sólido rígido para describir la orientación de un sistema de referencia solidario con un sólido rígido en movimiento.
Ecuaciones de Equilibrio.
Un sólido rígido está en equilibrio, respecto a un sistema de referencia inercial S, cuando la resultante de las fuerzas Fi aplicadas sobre él es nula y cuando el momento resultante respecto a un punto cualquiera O de S -que es la suma de los momentos de las fuerzas aplicadas Fi, respecto al punto O, más los momentos mj de los pares directamente aplicados- es también nulo, es decir:
F = ∑i Fi = 0
∑ Fx = 0 ∑ Fy = 0 ∑ Fz= 0 → F= m x a
∑ M0= ∑ (r x f )= 0
∑ Mx=0, ∑ M y=0, ∑ Mz=0.
Reacciones en los Soportes (Puntos de Apoyo) y en las Conexiones de una Estructura.
Los apoyos de vigas, son los elementos que le proporcionan la estabilidad a la viga y por lo general, se encuentran en los extremos o cerca de ellos. Las fuerzas en los apoyos que se generan son productos de las cargas aplicadas y se llaman reacciones y equilibran las cargas aplicadas. Analíticamente estas reacciones representan las incógnitas de un problema matemático. Las reacciones se pueden dividir en tres grupos que corresponden al tipo de apoyo que se está empleando:
- Reacciones equivalentes a una fuerza cuya línea de acción es conocida.
- Reacciones equivalentes a una fuerza de magnitud y dirección desconocidas.
- Reacciones equivalentes a una fuerza y un par.
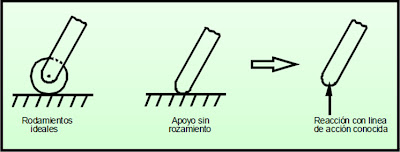
Reacciones Equivalentes a una Fuerza Cuya Línea de Acción es Conocida.
Los apoyos y conexiones que originan reacciones de este tipo incluyen: rodillos, balancines, superficies sin fricción, eslabones, cables cortos, collarines sobre barras sin fricción y pernos sin fricción en ranuras lisas. Cada uno de estos apoyos y conexiones pueden impedir movimiento sólo en una dirección.
Reacciones Equivalentes a una Fuerza de Magnitud y Dirección Desconocidas.
Los apoyos y conexiones que originan reacciones de este tipo incluyen: pernos sin fricción en orificios ajustados, articulaciones, bisagras y superficies rugosas. Estos pueden impedir la traslación del cuerpo rígido en todas las direcciones pero no pueden impedir la rotación del mismo con respecto a la conexión. En el caso de una superficie rugosa, la componente perpendicular a la superficie debe dirigirse alejándose de ésta.
Reacciones Equivalentes a una Fuerza y un Par
Estas reacciones se originan por apoyos fijos, los cuales se oponen a cualquier movimiento del cuerpo libre y, por lo tanto, lo restringen completamente. Los soportes fijos producen fuerzas sobre toda la superficie de contacto, sin embargo, estas fuerzas forman un sistema que se puede reducir a una fuerza y un par.
Diagrama de Cuerpo Rígido.
Esto se lleva a cabo seleccionando una partícula de interés y dibujando, por separado, un diagrama que muestre a dicha partícula y todas las fuerzas que están actuando sobre ella.
Fuerzas que Actúan Sobre el Cuerpo:
T1: Tensión en cuerda 1.
T2: Tensión en cuerda 2.
W: Peso del cuerpo.
Ejercicios Resueltos Unidad 3: Equilibrio de Cuerpos Rígidos:



No hay comentarios:
Publicar un comentario