Número complejo
El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i). Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física (y notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.
En matemáticas, los números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. La propiedad más importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas.
Los números complejos son una extensión de los números reales, cumpliéndose que ℝ ⊂ ℂ. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
Contienen a los números reales y los imaginarios puros y constituyen una de las construcciones teóricas más importantes de la inteligencia humana. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.
Definición: el numero imaginario i.
Sea el número i que cumple la relación siguiente
i2 = −1
El número i es llamado unidad imaginaria, y un número x sería imaginario puro si verifica la siguiente relación
x = bi
donde b ∈ ℝ.
Los números complejos ℂ son una extensión de los números reales ℝ, y se definen como la suma de un número real y un número imaginario puro de la forma
z = a + bi
donde {a, b} ∈ ℝ, y z ∈ ℂ.
Operaciones con números complejos
- Suma
Para sumar números complejos, se siguen las normas básicas de la aritmética, sumando los reales con los reales y los imaginarios con los imaginarios:
Ejemplo de suma:
- Resta
Al igual que en la suma, se opera como con los números reales ordinarios:
- Multiplicación
Para multiplicar dos números complejos, se multiplica cada término del primero por los dos del segundo, con lo que obtenemos 4 términos:
Obsérvese que el término bdi2 pasa a ser − bd. Eso es porque i2 = − 1. Ejemplo:y asi queda
- División
La división de números complejos requiere un mayor trabajo que la multiplicación y partimos de un artificio previo, basado en que el producto de un numero complejo por su conjugado da como resultado un número real:
si la división de dos números complejos, la multiplicamos y dividimos por el conjugado del denominador:
Para elevar un número complejo a un exponente entero, se aplican las identidades notables. Se debe tener en cuenta la igualdad i2 = − 1:
Valor absoluto o módulo de un número complejo
El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión:
Si pensamos en las coordenadas cartesianas del número complejo z como algún punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano a dicho punto.
Si el complejo está escrito en forma exponencial z = r eiφ, entonces |z| = r. Se puede expresar en forma trigonométrica como z = r (cosφ + isenφ), donde cosφ + isenφ = eiφ es la conocida fórmula de Euler.
Podemos comprobar con facilidad estas cuatro importantes propiedades del valor absoluto
para cualquier complejo z y w.
Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio métrico con los complejos gracias al que se puede hablar de límites y continuidad. La suma, la resta, la multiplicación y la división de complejos son operaciones continuas. Si no se dice lo contrario, se asume que ésta es la métrica usada en los números complejos.
Conjugado de un número complejo
Dos binomios se llaman conjugados si solo difieren en su signo central, por ejemplo, los dos binomios: 3m - 1 y 3m + 1 son conjugados.
El conjugado de un complejo z es un nuevo número complejo, definido así:
Se observa que ambos difieren en el signo de la parte imaginaria.
Con este número se cumplen las propiedades:
Esta última fórmula es el método elegido para calcular el inverso de un número complejo si viene dado en coordenadas rectangulares.
REPRESENTACIÓN GRÁFICA
Los números complejos se representan en el plano. Para ello se consideran los ejes coordenados y se representan en el eje de abscisas la parte real del número complejo y en el eje de ordenadas la parte imaginaria. Así, dado el número complejo a+bi, su representación en el plano se corresponde con el punto dado por el par (a, b). Y recíprocamente, dado un punto en el plano definido por el par (a, b), este punto representa el numero complejo a+bi.
Debido a la correspondencia biunívoca que se establece entre los números complejos y los puntos del plano, éste recibe el nombre de plano complejo, el eje de abscisas se llama eje real, y el eje de ordenadas, eje imaginario.
Propiedades
1. Los números complejos con parte imaginaria nula (números reales) se representan en el eje de abscisas.
2. Los números complejos con parte real nula (números imaginarios puros) se representan en el eje de ordenadas.
3. Un número complejo y su opuesto vienen representados en el plano por puntos simétricos respecto al origen.
4. Un número complejo y su conjugado vienen representados en el plano por puntos simétricos respecto al eje de abscisas.
Forma cartesiana de un número complejo
Los Números Complejos podemos imaginarlos como puntos de un plano (el plano de los números complejos). En ese plano podemos trazar unos ejes perpendiculares que nos sirvan de referencia para localizar los puntos del plano.
Lo habitual es utilizar las coordenadas del punto (x,y). Cuando representamos un número complejo de esta forma decimos que está en forma cartesiana
Tenemos un número complejo a+bi, su representación en el plano se corresponde con el punto dado por el par (a, b). Dado un punto en el plano definido por el par (a, b), este punto representa el numero complejo a+bi.
Podemos decir (a+bi)=(a,b)
Forma polar de un número complejo
La forma polar de un número complejo z, es aquella en que se da el módulo r y el argumento |z|.
Se representa por ℂ={ z =a + bi; a, b ∈ ℝ, i =√-1}.
Paso de forma binómica a forma polar
Para pasar un número complejo z = a + bi a forma polar z = rα es suficiente con hallar el módulo |z|= r = √(a2 + b2) y el argumento α y se denota por arg(z) y se calcula mediante la expresión:
Paso de forma polar a forma binómica
Para pasar un número complejo en forma polar z = rα a forma binómica es suficiente con hallar la parte real como a = r cosα y la parte maginaria como b = r senα .
La forma trigonométrica de un número
La forma trigonométrica es una variante de la forma polar, también utiliza el módulo y el argumento. Es muy útil para pasar de la forma polar a la forma binómica:
Dado un número complejo en forma polar, z = rα , para pasarlo a forma binómica, z = a+bi, hay que hallar las componentes a y b. Se utiliza la definición de seno y coseno.
Fórmula de de Moivre
La Fórmula de de Moivre nombrada así por Abraham de Moivre afirma que para cualquier número complejo (y en particular, para cualquier número real) x y para cualquier entero n se verifica que:
Esta fórmula es importante porque conecta a los números complejos (i significa unidad imaginaria) con la trigonometría. La expresión "cos x + i sen x" a veces se abrevia como cis x.
Sea z = r ( cosθ + i.senθ ) entonces
Zn[r ( cosθ + i.senθ )] ⟹ rn=( cos(nθ) + i.sen(nθ)
Siendo n cualquier entero.
Fórmula de Euler
La fórmula o relación de Euler, atribuida a Leonhard Euler, establece que:
para todo número real x. Aquí, e es la base del logaritmo natural, i es la unidad imaginaria y senx y cosx son funciones trigonométricas.
Ó bien:
siendo Z la variable compleja formada por : Z=a+ix.
Raíz de números complejos
La raíz enésima de número complejo es otro número complejo tal que:
Su módulo es la en raíz enésima del módulo.
Su argumento es:

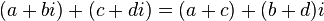





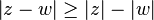


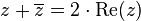



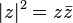



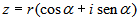
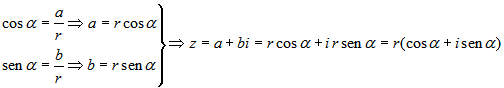
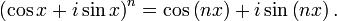
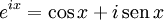
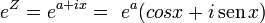



No hay comentarios:
Publicar un comentario