Introducción a la Integración en el Campo Complejo
El desarrollo de la teoría de funciones de una variable compleja sigue un camino muy distinto al usado en la teoría de funciones de variable real.
En esta última teoría, tras estudiar las funciones derivables, se estudian las funciones que admiten derivadas de órdenes superiores, luego las indefinidamente derivables y por último las que admiten desarrollo de Taylor en serie de potencias.
En la teoría de funciones de variable compleja, se comienza estudiando las funciones analíticas. Forman éstas una clase tan restringida que automáticamente admiten derivadas de cualquier orden en cada punto en que sean analíticas. Más aún, admiten desarrollo de Taylor, en un entorno de cada punto de analiticidad.
Pero supuesta f(z) analítica en un dominio, no ha sido posible demostrar la existencia de derivadas de órdenes superiores, sin recurrir a la integración compleja. En el desarrollo de Cauchy de la teoría de funciones de variable compleja, todo se hace depender del cálculo integral complejo, incluso en cuestiones que aparentemente sólo se refieren al cálculo diferencial.
Por tanto, constituyen una parte muy importante de la teoría de funciones de variable compleja, la teoría de las integrales curvilíneas, junto con la de series de potencias. Se caracterizan por su elegancia matemática y por su gran utilidad en la matemática tanto pura como aplicada.
Para definir la integral curvilínea o integral definida compleja a lo largo de una curva, es conveniente definir previamente la integral definida de una función compleja de variable real, en un intervalo.
Integral Definida de una Función Compleja de Variable Real.
Se trata de una generalización inmediata de la integral simple real.
a) Definiciones previas
- Una función compleja de variable real es una función de la forma:
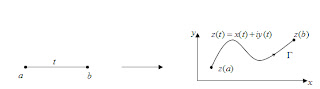
f(t) = u(t) + i v(t) ó z(t) = x(t) + i y(t) con t Î I = [a,b]
Dicha función se dice continua en I, si lo son x(t) e y(t).
Obsérvese que una tal función define una curva G en el plano complejo, recorrida en un sentido determinado.
La función anterior se dice continua a trozos en I, si x(t) e y(t) son continuas a trozos en I (Acotadas y continuas en I excepto en un número finito de puntos de discontinuidad de primera especie)
Se dice que z(t) = x(t) + i y(t) es derivable a trozos en I si lo son x(t) e y(t).
Se define entonces la función derivada como z´(t) = x´(t) + i y´(t)
Se dice que z(t) = x(t) + i y(t) es regular en I, o que lo es la correspondiente curva Γ, si existen x´(t) e y´(t) y son continuas y no nulas ambas en I.
Se dice que z(t) = x(t) + i y(t) es regular a trozos en I, o que lo es la correspondiente curva Γ, si x(t) e y(t). son continuas en I, existiendo y siendo continuas, x´(t) e y´(t). en I, excepto a lo sumo en un nº finito de puntos en los que deben existir y ser continuas las derivadas laterales.
Un contorno es una curva Γ regular a trozos y simple o de Jordan.
b) Definición
Dada la función compleja de variable real z(t) = x(t) + i y(t) continua a trozos en [a,b], se define la integral definida de z(t) sobre [a,b] como
c) Propiedades
De la definición y las propiedades de la integral definida de funciones reales de variable real, se deduce de forma inmediata, siendo z(t), z1(t), z2(t), continuas a intervalos en
I = [a,b]:
También se cumple:
Si la función compleja de variable real Z(t) verifica Z´(t) = z(t) , entonces:
Se verifica también:
Demostración:
Ahora el integrando es una función real de variable real y además:
Luego aplicando la correspondiente propiedad del caso real:
Integrales Curvilíneas Complejas o de Contorno
a) Definición
“Sea C un contorno descrito por C: z(t) = x(t) + i y(t) con t Î I = [a,b]
Sea f(z) una función compleja de variable compleja, continua sobre C.
La integral curvilínea compleja o integral de contorno de f(z) a lo largo del arco orientado C, que se representa por
se define así:
b) Comentarios
La integral del 2º miembro es integral de una función compleja de variable real t.
Existe esa integral, pues z(t) es continua en I y f(z) continua sobre C.
Luego f [z(t)] es continua en I y como z´(t) es continua en I excepto en un nº finito de puntos, el integrando es continua a trozos en I.
Si z´(t) no es continua sobre I, puede dividirse el intervalo I de forma obvia. Es decir si C está compuesto de un nº finito n de arcos regulares orientados Ci entonces:
c) Expresión en términos de integrales curvilíneas reales
De la definición:
Luego:
Puede escribirse
, desarrollando el integrando de acuerdo con las leyes algebraicas usuales.
d) Notas
Salvo indicación expresa, convenimos en que:
§ Los caminos de integración son contornos
§ Los integrandos son funciones continuas sobre esos contornos, o más generalmente continuas a intervalos
Por eso a la integral curvilínea se le designa integral de contorno.
El valor de la integral
es invariante si se sustituye la representación paramétrica z(t) t ∈ I, por otra equivalente en el sentido que se vió en las integrales curvilíneas reales , siempre que describa la curva en el mismo sentido. Si se describe en sentido opuesto cambia el signo de la integral.
Se deduce de la expresión en términos de integrales curvilíneas reales y de la invariancia de éstas ante el cambio de parámetros.
e) Propiedades
Se entiende que si C está descrita por z(t) t∈ [a,b] entonces -C está descrita por z(t) con t variando desde t = b hasta t = a. Queda entonces la curva recorrida en sentido contrario al de C.
Se entiende que si C1≡Z1 (t) t∈ [a,b] y C2≡z2 (t) t∈ [b,c] y siendo Z1 (b)=Z2 (b) se denota C1+C2 al contorno definido por
Puede generalizarse a donde con C_1+⋯+Cn se entiende la generalización obvia de la definición vista para C1+C2
La demostración de estas cuatro primeras propiedades se deduce de la definición de integral de contorno y las propiedades de la integral de funciones complejas de variable real.
f) Desigualdad ML
Si f(z) es continua a trozos sobre un contorn C ≡ z(t) t∈[a,b], y es M una cota superior de
en C y L la longitud de C, se verifica:
En efecto:
g) Notas
Si z recorre C, se interpreta |dz| como |dz|=|x´(t)+iy´(t) |dt
Por tanto, como la longitud de un contorno C≡z(t), t∈[a,b], es
, puede expresarse L de forma abreviada por
Puede hablarse también de integración respecto a la longitud del arco. Se representa por
y se define por:
Suelen considerarse integrales curvilíneas, respecto a z Se definen formalmente:
Con esta notación suelen introducirse:
Teorema de Cauchy-Goursat
a) Teorema de Cauchy-Goursat
Si f(z) es analítica sobre un contorno cerrado C y su interior, entonces
Es un teorema de gran importancia en la teoría de funciones de variable compleja.
Su demostración es complicada bajo esta forma general.
La forma original de Cauchy exige además la continuidad de f´(z) sobre C y su interior. Goursat fue el primero en mejorar el teorema, suprimiendo la hipótesis de la continuidad de f´(z), no necesaria para demostrar la tesis. Precisamente el ser f´(z) continua es una consecuencia que se demuestra a partir del teorema.
Veamos la demostración en la forma de Cauchy:
Sea R la región cerrada formada por C y su interior. Sea f(z) = u(x,y) + i v(x,y)
Por ser f(z) analítica en R, las u y v son continuas, derivables y cumplen las condiciones de Cauchy-Riemann en R.
Si añadimos que f´(z) sea continua en R, entonces las derivadas de u, v son continuas en R.
Es
Y por ser u, v continuas y con derivadas continuas en R es aplicable el teorema de Green-Riemann a cada una de las integrales curvilíneas reales. Resulta:
Y por cumplirse las condiciones de Cauchy-Riemann: ux = vy; uy = -vx , resulta:
c.q.d.
Teorema de Green
El teorema de Green establece la relación entre una integral de línea alrededor de una curva C cerrada y simple, y una integral doble sobre la región plana D limitada por C.
El teorema de Green se llama así por el científico británico George Green y es un caso especial del más general Teorema de Stokes.
El teorema de Green se llama así por el científico británico George Green y es un caso especial del más general Teorema de Stokes.
Este tipo de teoremas resulta muy útil ya que dados un campo vectorial y una curva cerrada simple sobre cual hay que integrarlo, podemos elegir la posibilidad mas simple entre poder integrar el campo directamente sobre la curva o bien integrar la diferencia de sus derivadas parciales cruzadas sobre el recinto que este delimitando la curva.
Por otra parte, la relación así establecida entre la integral de la línea sobre una curva y la integral doble sobre la región interior a ésta, permite a veces obtener información sobre una función o su integral en un espacio a partir del comportamiento de esta función sobre la frontera de dicho recinto.
Teorema de Green
Sea C una curva simple y cerrada, suave a trozos y orientada positivamente, y sea F(x;y) = (P;Q) un campo vectorial cuyas funciones coordenadas tienen derivadas parciales continuas sobre una región abierta que contiene a la región D acotada por C. Entonces:
Demostración del Teorema de Green
Notase que el Teorema de Green quedará demostrado si se prueba que
Para demostrar la ecuación 1 expresemos D como una región tipo I:
Donde g1 y g2 son funciones continuas. Esto permite calcular la doble integral del lado derecho de la ecuación 1 como sigue:
donde en el último paso se sigue el teorema fundamental del cálculo.
Ahora calculamos el lado izquierdo de la ecuación 1 descomponiendo C como la unión de las cuatro curvas C1, C2, C3 y C4 como se muestra en la figura. En C1 tomamos x como el parámetro y escribimos las ecuaciones para-métricas como x=x y
Entonces:
Observe que C3 va de derecha a izquierda, pero –C3 va de izquierda a derecha, de modo que podemos escribir las ecuaciones para-métricas de –C3 como
Por lo tanto:
En C2 y C4, x es constante, de modo tal que dx=0 y
Por lo tanto,
Comparando esta expresión con la de la ecuación 3, vemos que,
La ecuación 2 se puede probar en forma muy semejante al expresar D como una región tipo II. Entonces sumando las ecuaciones 1 y 2, obtenemos el Teorema de Green.
El teorema de Green se cumple aún para regiones S que tengan uno o más hoyos, siempre que cada parte de la frontera esté orientada de modo que S quede siempre a la izquierda cuando se sigue la curva en su dirección positiva. Basta con descomponerla en regiones ordinarias.




































No hay comentarios:
Publicar un comentario