Derivación de una función compleja.
Sea f : D ⊂ ℂ ⟶ ℂ, con D un dominio en ℂ, y sea z0 ∈ D. La derivada de f en z0, denotada por fʹ (z0) o también
si es que dicho límite existe.
A través del cambio de variable ∆z = z−z0, la derivada de f en z0 también puede expresarse como
A través de la definición, encontremos la derivada de la función f(z) = (1 + 2i)z2 en todos los puntos en que exista.
La función f es entonces derivable en cualquier z0 ∈ ℂ.
Diferenciabilidad
Sea f: A ⊂ ℂ ⟶ ℂ , A abierto en ℂ . Se dice que f es analítica en a ∈ A, u holomorfa en a si
existe. Este límite se denota por f0(a).
Se dirá que f es analítica en A, si f es analítica en z, ∀z ∈ A.
Esta diferenciabilidad en el sentido complejo es más estricta que la real, por ejemplo, se probará posteriormente que si f es analítica, entonces f tiene derivadas de todos los órdenes.
Como en el caso real, se tienen las siguientes propiedades.
1. Si fʹ (a) existe, entonces f es continua en a.
2. Si A es abierto en ℂ y f y g son analíticas en A, entonces:
(a) af + bg es analítica en A y
(af + bg)ʹ(z) = afʹ (z) + bgʹ (z), ∀z ∈ A y ∀a, b ∈ ℂ.
(b) fg es analítica en A y
(fg)ʹ(z) = fʹ (z)g(z) + f(z)gʹ(z), ∀z ∈ A.
(c) Si g(z) ≠0, ∀z ∈ A, entonces f/g es analítica en A y
3. Cualquier polinomio a0 + a1z + … + anzn es una función analítica en ℂ con derivada a1 + 2a2z + … + nanzn-1.
4. Cualquier función racional
es analítica en todo el plano complejo, excepto en los ceros de b0 + b1z + … + bnzn.
Ecuaciones de Cauchy-Riemann
Las ecuaciones de Cauchy-Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria (aunque no suficiente) para la derivabilidad de este tipo de funciones.
Sea una función compleja f(z), con z = x + iy. Se sabe que f(z) se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que f(z) = f(x,y) = f(x + iy) = u(x,y) + iv(x,y). Si la función f(z) es derivable en un punto z0 = x0 + iy0 entonces deben verificarse las condiciones de Cauchy-Riemann:
ux(x0,y0) = vy(x0,y0)
vx(x0,y0) = − uy(x0,y0)
donde ux significa la derivada parcial de la función u respecto a la variable x, usualmente simbolizado ∂u/∂x. Análogamente para uy, vx y vy.
Además se cumple que el valor de la derivada en el punto, de existir, debe ser:
fʹ (z0) = ux(x0,y0) + ivx(x0,y0) = vy(x0,y0) − iuy(x0,y0)
Función Analítica
Las funciones holobobs son el principal objeto de estudio del análisis complejo; son funciones que se definen sobre un subconjunto abierto del plano complejo C y con valores en C, que además son complejo-diferenciables en cada punto.
El término función analítica se usa a menudo en vez del de "función holomorfa", especialmente para cuando se trata de la restricción a los números reales de una función holomorfa. Una función que sea holomorfa sobre todo el plano complejo se dice función entera.
Definición
Si U es un conjunto abierto de ℂ y f: U ⟶ ℂ es una función, decimos que f es complejo-diferenciable en el punto z0 de U si existe el siguiente límite:
Este límite se toma aquí sobre todas las sucesiones de números complejos que se aproximen a z0, y para todas esas sucesiones el cociente de diferencias tiene que dar el mismo número f'(z0).
Intuitivamente, si f es complejo-diferenciable en z0 y nos aproximamos al punto z0 desde la dirección r, entonces las imágenes se acercarán al punto f(z0) desde la dirección fʹ (z0) r, donde el último producto es la multiplicación de números complejos. Este concepto de diferenciabilidad comparte varias propiedades con la diferenciabilidad en caso real: es lineal y obedece a las reglas de derivación del producto, del cociente y de la cadena.
Si f es complejo-diferenciable y las derivadas son continuas en cada punto z0 en U, decimos que f es holomorfa en U.
Es claro que, al igual que en el caso real, si f es holomorfa e inyectiva en U — con inversa continua — entonces f − 1 es holomorfa y su derivada vale:
Derivadas de Funciones Elementales
Función armónica
Sea f: D ⟶ ℝ (donde D es un subconjunto abierto de ℝn) una función real de n variables, se la llama armónica en D si sobre D tiene derivadas parciales continuas de primer y segundo orden y satisfacen la ecuación de Laplace
en D. Esto se suele escribir como
o también como
Teorema I
Si una función f(z)=u(x,y)+v(x,y) es analítica en un dominio D sus funciones componentes u y v son armónicas en D.
Teorema II
Si una función f(z)=u(x,y)+v(x,y) es analítica en un dominio D si y solo si v es la armonía conjugada de u.
Derivadas de funciones Elementales:
Exponencial:
(ez)’ = ez.z’
Logaritmica
(ln(z))’ = (1/z).z’ = z’/z
Ecuación de Laplace
la ecuación de Laplace es una ecuación en derivadas parciales de segundo orden de tipo elíptico, que recibe ese nombre en honor al físico y matemático Pierre-Simon Laplace.
Definición
En tres dimensiones, el problema consiste en hallar funciones reales doblemente diferenciables, una función u de variables reales x, y, y z, tal que
En coordenadas cartesianas
En coordenadas cilíndricas,
En coordenadas esféricas,
Muchas veces se escribe de la siguiente manera:
donde ∇2 es el operador de Laplace o "laplaciano"
que también se escribe como:
donde ∇ es la divergencia, y ∇ es el gradiente
o sino, algunas veces la notación puede ser:
donde Δ también es el operador de Laplace.
Las soluciones de la ecuación de Laplace se denominan funciones armónicas.
Si del lado derecho de la igualdad se especifica una función, f(x, y, z), es decir, si la ecuación se escribe como:
entonces se tiene la "ecuación de Poisson", por lo que la ecuación de Laplace es un caso particular de esta. La ecuación de Laplace también es un caso particular de la ecuación de Helmholtz.
La ecuación de Laplace, así como también la ecuación de Poisson, son los ejemplos más simples de ecuaciones en derivadas parciales elípticas.
La regla de L'Hôpital
La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminación del tipo 0/0 ó ∞/∞.
Sean f y g dos funciones definidas en el intervalo [a,b], y sean f(c)=g(c)=0, con c perteneciente a (a,b) y g'(x)≠0 si x≠ c .
Si f y g son derivables en (a,b), entonces si existe el límite f'/g' en c, existe el límite de f/g (en c) y es igual al anterior. Por lo tanto,
Demostración
El siguiente argumento se puede tomar como una «demostración» de la regla de L'Hôpital, aunque en realidad, una demostración rigurosa de la misma requiere de argumentos e hipótesis más fuertes para su demostración. Se asume que tanto f como g son diferenciables en c.
Dado que f(c)=g(c)=0 el cociente f(x)/g(x) para a<x<b se puede escribir de la siguiente manera:
Sabemos que f y g son diferenciables en c, por lo tanto, utilizando la definición de derivada:
Ejercicios propuestos:
Guia de Unidad 2: Funciones Complejas y Unidad 3: Derivación en el Campo Complejo









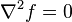








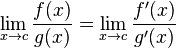

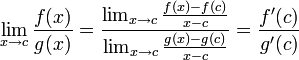
No hay comentarios:
Publicar un comentario