Transformada de Laplace
La transformada de Laplace de una función f(t) definida (en matemáticas y, en particular, en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:
siempre y cuando la integral esté definida. Cuando f(t) no es una función, sino una distribución con una singularidad en 0, la definición es
Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:
La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).
Propiedades
Linealidad
Derivación
Integración
Dualidad
Desplazamiento de la frecuencia
Desplazamiento temporal
Nota: u(t) es la función escalón unitario.
Desplazamiento potencia n-ésima
Convolución
Transformada de Laplace de una función con periodo p
Condiciones de convergencia
ℒ{(et²)}(que crece más rápido que e−st) no pueden ser obtenidas por Laplace, ya que et², no es una función de orden exponencial de ángulos.
Tabla de las transformadas de Laplace más comunes
La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable.
Debido a que la transformada de Laplace es un operador lineal, la transformada de Laplace de una suma es la suma de la transformada de Laplace de cada término.
Aquí está una lista de las transformadas más comunes. En ella u denota a la llamada función de Heaviside o función escalón, que vale 1 cuando su argumento es positivo y 0 cuando su argumento es negativo. Cuando su argumento vale 0 se le suele asignar el valor 1/2, aunque esto no tiene relevancia práctica.
Función Heaviside
La función escalón de Heaviside, también llamada función escalón unitario, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo.
Tiene aplicaciones en ingeniería de control y procesamiento de señales, representando una señal que se enciende en un tiempo específico, y se queda prendida indefinidamente.
Definición
En ingeniería es común encontrar funciones que corresponden a estados de sí o no, o bien activo o inactivo. Por ejemplo, una fuerza externa que actúa sobre un sistema mecánico o una tensión eléctrica aplicada a un circuito, puede tener que suspenderse después de cierto tiempo. Para tratar de forma efectiva con estas funciones discontinuas conviene introducir una función especial llamada función escalón unitario o función Heaviside.
La función Heaviside, es una función discontinua cuyo valor es 1 para el argumento positivo y 0 en el resto del intervalo.
Definimos H(t-a) sólo en el eje t no negativo puesto que es todo lo que nos interesa en el estudio de la transformada de Laplace.
En el sentido más amplio, H(t-a) = 0cuando t < a. Cuando una función f definida para t ≥0 se multiplica por H(t-a) , la función escalón unitario "desactiva" una porción de la gráfica de esa función.
Propiedades
- Cambio de signo del argumento.
- La derivada en el sentido de las distribuciones es la Función Delta de Dirac.
- Transformada de Laplace.
- Límites.
- Es la integral de la Función Delta de Dirac.
El valor de H(0) es causa de discusión. Algunos lo definen como H(0) = 0, otros H(0) = 1. H(0) = 1/2 es la opción usada más coherente, ya que maximiza la simetría de la función, y permite una representación de la misma a través de la función signo:
Puede especificarse con un subíndice el valor que se va a usar para H(0), de la siguiente forma: Plantilla:Ecuación Una forma de representar esta función es a través de la integral
Convolución y transformadas
La transformada de Laplace es lineal, es decir, la transformada de una suma es la suma de las transformadas, entonces cabe preguntarse si se tiene algo similar para el producto, la respuesta es no. En general la transformada no conmuta con la multiplicación ordinaria, o sea, la transformada de un producto no es el producto de las transformadas, pero podemos definir un nuevo producto generalizado bajo el cual esto es cierto.
Definición
La función h: C(I) ⨉ C(I) ⟶ C(I), donde C es el conjunto de funciones continuas en el intervalo I=[0, +∞ [ dada por
se conoce como la convolución de f y g.
La convolución tiene muchas de las propiedades de la multiplicación ordinaria, como veremos en el siguiente teorema.
Propiedades de la Convolución
Sean f y g funciones continuas en el intervalo I=[0, +∞ [, entonces
Transformada de Derivadas e Integrales
Transformada de derivadas
Sea f(t) continua en (0,∞) y de orden exponencial a y sea f´ seccionalmente continua en [0,∞).
Entonces
ℒ[f´(t)] = s F(s) - f(0+), (s > a)
Si se cumplen las condiciones anteriores, salvo que f(t) tiene discontinuidad por salto en t = a > 0 , entonces :
ℒ[ f´(t)] = s F(s) - f(0+) - e-as [f(a+)-f(a-)]
Análogo si existen varias discontinuidades por salto.
Si f, f’ , ... , f(n-1) son continuas en (0,∞) y de orden exponencial a y f(n) es seccionalmente continua en [0,∞), entonces :
ℒ[f(n) (t)] (s) = sn F(s) - sn-1 f(0+) - sn-2 f’(0+) - ··· - f(n-1) (0+) , (s > a)
Así para n = 2
ℒ[f’’ (t)] = sℒ [f’] - f’ (0+) = s [ s F(s) - f (0+)] - f’(0+)
ℒ[f’’ (t)] = s2 F(s) - s f (0+) - f’(0+).
En general, inducción.
Aquí se intuye la utilidad de la transformada de Laplace para resolver problemas de valor inicial. Se reemplaza la “derivación respecto a t “, por “multiplicación por s”, transformándose una ecuación diferencial con coeficientes constantes, en una algebraica.
b) Transformada de integrales
Demostración para el caso particular en que f sea continua en [0,∞):
Transformada inversa de Laplace
Al aplicar la transformada de Laplace a una ecuación diferencial la convertimos en una ecuación algebraica, la cual podemos resolver para Y(s), es decir, Y(s) = G(s). Ahora, como ℒ {y(t)}= Y(s), si pudiéramos devolvernos obtendríamos la solución y(t) que buscamos. Es decir, necesitamos de la transformada inversa ℒ-1{ Y(s) }, para hallar la función y(t)
Entonces definamos la transformada inversa.
Definición
Si F(s) es la transformada de Laplace de una función continua f(t), es decir, ℒ{f(t)}=F(s), entonces la transformada inversa de Laplace de F(s), escrita ℒ-1{ F(s)} es f(t) , es decir, ℒ-1{ F(s)} = f(t).
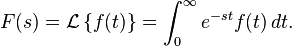
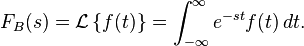

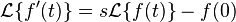

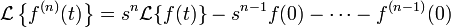




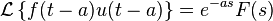

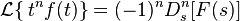


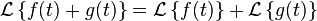













No hay comentarios:
Publicar un comentario