Impulso.
El impulso es el producto entre una fuerza y el tiempo durante el cual está aplicada. Es una magnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo, por lo tanto si la fuerza es constante el impulso se calcula multiplicando la F por Δt, mientras que si no lo es se calcula integrando la fuerza entre los instantes de tiempo entre los que se quiera conocer el impulso.
Cantidad de Movimiento.
La cantidad de movimiento es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
m= Masa
v= Velocidad (en forma vectorial)
p =Vector cantidad de movimiento.
Choques Elásticos e Inelásticos
La conservación de la cantidad de movimiento encuentra su mayor aplicación en el estudio de la interacción, en las cuales dos o más cuerpos ejercen mutuamente fuerzas muy grandes que duran, sin embargo un intervalo de tiempo muy pequeño. Dichas fuerzas se denominan fuerzas impulsivas, y aparecen, por ejemplo cuando una pelota de futbol choca con el pie de un jugador, éste es un ejemplo típico de fuerza impulsiva.
Los choques entre dos partículas, por ejemplo, entre dos bolas de billar se acostumbra clasificarlas de la siguiente manera: si las partículas se mueven sobre una misma recta, antes y después de la colisión, decimos que el choque es central o directo.
Si esto no ocurre, decimos que la condición es oblicua. Por otra parte, si la energía cinética de las partículas, antes de la colisión, es igual a la energía cinética total, después de la colisión, decimos que el choque es elástico. En una condición elástica, la energía cinética se conserva. En caso contrario la colisión es inelástica. La energía cinética final podrá ser mayor o menor que el inicial.
Si la energía cinética aumenta, hay forzosamente una fuente de energía que proporciona este aumento, durante la interacción si la energía cinética disminuye puede haber aparición de calor o deformaciones permanentes en los cuerpos que chocan. Finalmente, si las partículas después de la colisión se mueven con la misma velocidad, tenemos una colisión completamente inelástica, por ejemplo, cuando dos automóviles chocan y continúan adheridos después del choque.
Si la colisión fuere elástica, la conservación de energía cinética nos daría una ecuación más. Notemos sin embargo que debido a la naturaleza de las fuerzas impulsivas, podemos utilizar la conservación de la cantidad de movimiento, aunque la fuerza externa no sea nula.
Movimiento Cinético de una Partícula
El estudio de la Dinámica consta de dos partes: la Cinemática que estudia cómo se mueven los cuerpos y la Cinética que estudia la relación entre el movimiento y las fuerzas que lo originan. La Cinemática describe cómo varean la velocidad y la aceleración de un cuerpo con el tiempo y con sus cambios de posición. La buena comprensión de la Cinemática no sólo constituye un fundamento necesario para el posterior estudio de la Cinética. Sino que es, en sí misma, un importante campo de estudio. El proyecto de muchas piezas de maquinaria que deban crear movimientos concretos se basa casi exclusivamente, en la Cinemática. También se basa en ella el estudio del movimiento de proyectiles, naves espaciales y satélites artificiales.
Un sistema de partículas es un conjunto de partículas con alguna característica común que permita delimitarlo y en el que la posición y movimiento de una partícula depende de la posición y movimiento de las demás.
Generalidades Sobre el Choque.
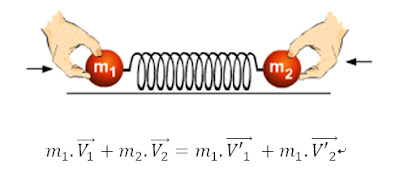
Se llama choques a la interacción de dos (o más) cuerpos mediante una fuerza impulsiva. Los choques son interacciones de dos o más cuerpos en el que existe contacto entre ellos durante un tiempo tanto determinado como indeterminado. Existen distintos tipos de choque, los choques elásticos, inelásticos y totalmente inelásticos. Todos estos choques tienen la característica de conservar su momento o cantidad de movimiento, pero no así su energía mecánica, que en la mayoría de los casos solo se considera la energía cinética. Si m1 y m2 son las masas de los cuerpos, entonces la conservación de la cantidad de movimiento establece que:
Donde:
son las velocidades iniciales y finales de las masas m1 y m2.
Características en los Choques
1) Los dos cuerpos pueden desintegrarse en pedazos
2) Puede haber una transferencia de masa
3) Las dos masas se pueden unir para formar una sola
4) Las masas pueden permanecer invariables. Aun en este caso hay diversas posibilidades. Los cuerpos pueden permanecer completamente inalterados, como cuando chocan dos bolas de billar, o bien se pueden deformar, como cuando chocan dos automóviles.
Efectos de Choque
La Mecánica de choque tiene el potencial de dañar, deformar, etc:
- Un frágil cuerpo puede fracturar. Por ejemplo, dos copas de cristal pueden romperse en caso de colisión una contra la otra. Una cizalla en un motor está diseñada para la fractura con una magnitud de choque.
- Un objeto dúctil se puede doblar por una conmoción. Por ejemplo, una jarra de cobre se puede curvar cuando cae en el suelo.
- Algunos artículos no pueden ser dañados por un solo choque, pero se produce fatiga con numerosos fracasos repetidos de bajos niveles choques.
- Un choque puede resultar en sólo daños menores que no pueden ser críticos para su uso. Sin embargo, los daños acumulados menores de varios choques eventualmente el resultado del objeto sería inutilizable.
- Un choque puede no producir daño aparente de inmediato, pero podría reducir la vida útil del producto: la fiabilidad se reduce.
- Algunos materiales como los explosivos se pueden detonar con mecánicas de choque o impacto.
Choque Elástico.
En física, en el caso ideal, una colisión perfectamente elástica es un choque entre dos o más cuerpos que no sufren deformaciones permanentes debido al impacto. En una colisión perfectamente elástica se conservan tanto el momento lineal como la energía cinética del sistema. Claro está que durante una colisión, aunque sean de dos sólidos, no se puede considerar perfectamente elástico ya que siempre hay una deformación.
Las colisiones en las que la energía no se conserva producen deformaciones permanentes de los cuerpos y se denominan colisiones inelásticas. Colisiones elásticas son aquellas en las cuales no hay intercambio de masa entre los cuerpos que colisionan, sin embargo, hay conservación neta de energía cinética.
Choque Inelástico.
Un choque inelástico es un tipo de choque en el que la energía cinética no se conserva. Como consecuencia, los cuerpos que colisionan pueden sufrir deformaciones y aumento de su temperatura. En el caso ideal de un choque perfectamente inelástico entre objetos macroscópicos, éstos permanecen unidos entre sí tras la colisión. El marco de referencia del centro de masas permite presentar una definición más precisa.
La principal característica de este tipo de choque es que existe una disipación de energía, ya que tanto el trabajo realizado durante la deformación de los cuerpos como el aumento de su energía interna se obtiene a costa de la energía cinética de los mismos antes del choque. En cualquier caso, aunque no se conserve la energía cinética, sí que se conserva el momento lineal total del sistema.
En una dimensión, si llamamos v1,i y v2,i a las velocidades iniciales de las partículas de masas m1 y m2, respectivamente, entonces por la conservación del momento lineal tenemos:
y por tanto la velocidad final vf del conjunto es:
Para el caso general de una colisión perfectamente inelástica en dos o tres dimensiones, la fórmula anterior sigue siendo válida para cada una de las componentes del vector velocidad.
Coeficiente de Restitución
El coeficiente de restitución es una medida del grado de conservación de la energía cinética en un choque entre partículas clásicas. En una colisión frontal alineada de dos esferas sólidas (como las que experimentan las bolas de billar) las velocidades después del choque están relacionadas con las velocidades antes del choque, por la expresión:
Donde "e" es precisamente el coeficiente de restitución, que toma valores entre 0 y 1. El valor 1 se da en un choque perfectamente elástico, donde se conserva tanto el momento lineal como la energía cinética del sistema. El valor 0 se da en un choque perfectamente inelástico, donde sólo se conserva el momento lineal, una porción de la energía cinética inicial de las partículas se "consume" durante el choque, convirtiéndose en energía de deformación plástica y en sonido. El coeficiente de restitución es la velocidad relativa de alejamiento, dividido entre la velocidad relativa de acercamiento de las partículas.
Línea de Choque: Recta soporte de las percusiones. U es el unitario.
Choque Excéntrico: La línea de choque no pasa por los centros de masas de las partículas. No se estudia. Véase dibujo previo.
Choque Central: La línea de choque pasa por los centros de masas de las partículas.
Choque Central Directo: Las velocidades antes y después de la colisión son paralelas a la línea de choque.
Choque Central Oblicuo: Las velocidades antes y después de la colisión no son paralelas a la línea de choque.
Plano de Choque (Partículas puntuales): Plano que contiene a la línea de choque y que definen las velocidades antes de la colisión.
Línea Normal: Línea perpendicular a la de choque contenida en el plano de choque u es el vector unitario.
Cinética del Sistema Variable de Partículas:
Corriente Estacionria de Partículas.
En mecánica consideramos un sistema de partículas como un conjunto de N puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas. Cada una de las partículas del sistema posee una masa propia, mi, siendo i = 1,…, N un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición ri y una velocidad vi. Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica.
siendo Fi la resultante de las fuerzas que actúan sobre la partícula i. Esta resultante se compone de las fuerzas que cada una de las demás partículas del sistema ejerce sobre i, más la resultante de las fuerzas externas aplicadas sobre ella
Este sumatorio representa la suma sobre las partículas restantes, esto es k va de 1 hasta N, excluyendo el caso k = i, ya que admitimos que una partícula no produce fuerza sobre sí misma (equivalentemente, Fi→i = mathbf0).
Suponemos que las interacciones entre las partículas obedecen la 3ª ley de Newton
o, lo que es lo mismo
En la mayoría de los casos se cumplirá además que la fuerza que la partícula k ejerce sobre la i (y por tanto la que la i ejerce sobre la k) va en la dirección de la recta que une
ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector Fk→ies paralelo a la posición relativa ri - rk esto es, si
Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición.
Sistema con Ganancia o Pérdida de Masa
En muchos problemas de Dinámica en un volumen de control penetran (o salen) partículas a razón contacto durante cierto intervalo de tiempo. Por ejemplo en la propulsión de un cohete el volumen de control puede ser el casco del cohete más el combustible no quemado. A medida que se quema el cohete lo expulsa y sale del volumen de control.
El sistema no sólo disminuye su masa al salir las partículas de él sino que las expulse a cierta velocidad relativa al resto del sistema. Por tanto, la cantidad de movimiento del sistema puede variar.
El otro tipo que se analizará de sistema de masa variable es aquel que gana masa por acoplo de partículas (como en recolector móvil que se va llenando de agua o grano) o que la pierda por ir expulsándola (como un cohete quemando el combustible).
Ejercicios Resueltos Unidad 10: Impulso y Cantidad de Movimiento



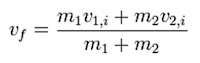












No hay comentarios:
Publicar un comentario