Residuo:
Se denomina Residuo de una función en un punto z0, y lo representamos por Resf(z0), a la magnitud
Donde R > 0 es tan pequeño como queramos. El cálculo del residuo en un punto involucra el cálculo de una integral a lo largo de un circuito cerrado que rodea al punto seguida de un límite R → 0.
Si el punto z0 es un punto regular de f(z) su residuo en z0 es nulo. Para el cálculo del residuo de una función en el punto del infinito se define mediante:
Teorema de los Residuos
Si una función f(z), analítica en una región R salvo tal vez en un conjunto finito de puntos singulares
zi, i = 1,…….,k, entonces si C es un circuito cerrado contenido en R y que encierra a los anteriores
k puntos singulares, se tiene que
Si el punto z0 es un polo simple, entonces
Si el punto z0 es un polo de orden n, entonces
Ejemplo: Determine el residuo de
en cada uno de los polos en el plano finito z y luego calcule la integral
Solución:
Factorizando el denominador tenemos
así que f(z)tiene polos simples en z=0; z=1
Ahora se obtienen los residuos usando la ecuación
Residuo en z=0
Residuo en z=1
Ahora para calcular la integral
se utiliza
entonces:
Ejemplo: Evalúe la integral de contorno;
donde C es el circulo |z|=3
Solución: Los polos son: un polo de orden 3 en z=0 y dos polos simples en z=-1 ± i, todos dentro del contorno C.
El residuo en z=0 está dado por:
Se deriva
quedándonos;
Ahora se vuelve a derivar
El residuo en z=-1-i es;
El residuo en z=-1+i es;
Asi al evaluar la integral por el teorema de los residuos, nos queda:
Cálculo de integrales reales mediante residuos
La aplicación más importante del teorema de los residuos es el cálculo de ciertos tipos de integrales reales. La idea básica es relacionar esas integrales reales con otras integrales sobre un contorno cerrado en el plano complejo, evaluar esta última mediante residuos y utilizar el resultado para deducir el valor de la primera.
En análisis real, la integral impropia de una función continua f(x) sobre el intervalo semi-infinito ≥0 se define como:
cuando existe el limite a la derecha, se dice que la integral impropia converge; y su valor es el valor de dicho límite.
Si f(x) es contínua para todo x, la integral impropia
se define como
Donde C es el contorno cerrado, que consiste del eje real de –R a +R y el semicírculo CR, de radio R en el semiplano superior z. Como z=x es el eje real.
Entonces, suponiendo que
NOTA: Para que ésta integral
tienda a cero a medida que , el grado del denominador de la función racional f(x)debe ser al menos dos veces mas grande que el grado del numerador.
Cuando existen ambos límites individuales, la integral converge, siendo su valor la suma de estos dos límites. Otro valor asignado a esta integral es el valor principal de Cauchy (P.V), que es:
Cuando
converge, el valor principal coincide con ella; pero también hay funciones, como f(x) = x, para las que no existe la integral y sí su valor principal. Ahora bien, si f es par, es decir f(−x) = f(x), entonces la integral en [0,∞) converge si y solo si converge su valor principal, ya que
Integrales de funciones de senos y cosenos
Consideremos la integral
donde F(x, y) es cualquier función real de dos variables tal que el integrando sea una función continua de θ en [0, 2π]. La forma de la integral sugiere la parametrización de la curva z(θ) = eiθ, con
0 ≤ θ ≤2π, es decir, la circunferencia unidad con orientación positiva C. Como z′(θ) = iz(θ),
sen θ = (z − z−1)/2i y cos θ = (z + z−1)/2,
La condición de que F(sen θ, cos θ) sea continua en [0, 2π] implica que el integrando de esta integral de contorno no tiene singularidades sobre C, de modo que, en principio, esta integral se puede hacer por residuos.










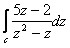




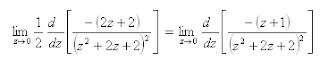















No hay comentarios:
Publicar un comentario