Función compleja de variable compleja
Una función compleja de variable compleja es una función f que va de un subconjunto D (no vacío) de los números complejos a los números complejos. Es común llamar z a la variable independiente y w = f(z) a la dependiente. Simbólicamente:
f : D ⊂ ℂ ⟶ ℂ
z ⟶ w = f (z)
El conjunto D se llama dominio de definición de f. Adoptaremos la convención de que si D no está explícitamente especificado, se sobreentiende que es el más grande subconjunto de ℂ para el cual la expresión que corresponde a f(z) está definida.
Es usual considerar expresados a z y w en su forma binómica, digamos z = x+iy y w = u+iv (con x, y, u, v ∈ ℝ). En general, las partes real e imaginaria de w dependerán tanto de x como de y, y para obtenerlas habrá que reemplazar a z por x + iy en la expresión que define a f(z) en términos de z, y operar hasta que quede claro cuáles son u y v reales en términos de x e y.
Dada una función compleja f, siempre podemos obtener la función parte real u : D ⊂ ℝ2 ⟶ ℝ y la función parte imaginaria v : D ⊂ ℝ2 ⟶ ℝ. Recíprocamente, cualquier par de funciones reales de dos variables u(x, y) y v(x, y) con dominio D ⊂ ℝ2 define una función f(z) = f(x + iy) = u(x, y) + iv(x, y) en el mismo dominio D (visto como subconjunto de ℂ).
Para cualquier función compleja f, el conocimiento de las funciones de parte real e imaginaria u y v será importante en el estudio de las propiedades de f (a título de ejemplo, nótese que f está definida en x0 +iy0 si, y sólo si, u y v están definidas en (x0, y0)). Por eso es esencial saber encontrarlas.
Funciones elementales
- Función Exponecial
Como en el caso real, la función exponencial puede ser definida como una función holomorfa en el plano complejo de diferentes maneras. Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales. Específicamente, la forma más usual de definirla para el dominio de los números complejos es mediante la serie de potencias, donde el valor real x se sustituye por la variable compleja z:
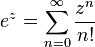
para valores imaginarios puros se cumple la identidad
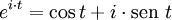 ,
,en el que un caso particular es la identidad de Euler, conocida también como la fórmula más importante del mundo.
Usando la identidad anterior, donde ahora z=x+yi, con x e y números reales, se obtiene una definición equivalente a la primera,
relación que demuestra que esta función, además de ser holomorfa, es periódica, con un periodo para la parte imaginaria de 2πi.
 |
| Gráfico de la parte real de una función exponencial en el campo de los complejos |
- Función Logarítmica
El logaritmo natural de un número complejo z es otro número complejo b = ln(z) que sea solución de la ecuación:
La ecuación anterior no tiene solución única. De hecho, tiene un número infinito de soluciones, aunque todas ellas son fáciles de encontrar. Dado un número complejo z escrito en forma polar, una solución posible de la ecuación () es b0:

Puede comprobarse que ésta no es la única solución, sino que para cualquier valor k ∈ ℤ resulta que el número complejo bk, definido a continuación, también es solución:

De hecho cada valor particular de k define una superficie de Riemann.
- Funciones Trigonométricas
El seno y coseno se definen en números complejos, gracias a la fórmula de Euler como:


Por lo tanto, la tangente quedará definida como:
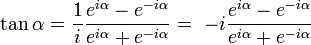
Siendo i=√ (-1) (también puede representarse como j).
- Funciones Hiperbólicas
El seno y coseno hiperbólicos se definen de la siguiente forma en en números complejos:
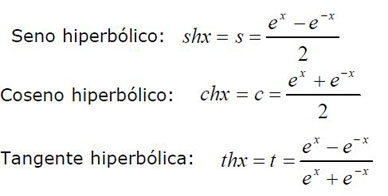
Limites de una función de variable compleja
Al concepto de limite de una función de variables complejas es análogo al concepto de limite de una función de variable real.
Sea f una función de D ⊂ ℂ en ℂ, z0 un punto de acumulación de D y L ∈ ℂ. Decimos que el límite de f cuando z tiende a z0 es L si ∀ε > 0, ∃δ > 0 : ∀z ∈ D, 0 <|z - z0| < δ ⇒ |f(z) - L|< ε.
En ese caso, escribimos

Por lo tanto todas las propiedades de los limites de las funciones vectoriales pueden aplicarse al límite de funciones completas, pudendo afirmar las siguientes propiedades.
Propiedades
a) El limite, si existe es único.
b) Si

y

Entonces

Sea
f(z)= u(x,y) + iv(x,y)
Z=x0+iy0
L=U0+iV0
Tenemos que

entonces

Generalizaciones

Continuidad de una función compleja
Una función f : D ⊂ ℂ ⟶ ℂ es continua en z0 ∈ D si ∀ε >0, ∃δ > 0 :∀z ∈ D, |z - z0| < δ ⇒ |f(z) - f(z0)| < ε. Si f es continua en todo punto de un subconjunto E, decimos que f es continua en E.
Analizando con cuidado la definición, podemos notar que si z0 es punto aislado en D, f es continua en z0. Si, por el contrario, z0 es punto de acumulación de D, se tiene que f es continua en z0 si, y sólo si, se satisfacen las siguientes tres condiciones simultáneamente:

Tipos de discontinuidad
- Evitable: se puede redefinir la función.
- Esencial: el límite no existe.

Continuidad uniforme
Analizando la definición de continuidad, podemos observar que una función es continua en un subconjunto S de su dominio si
∀z ∈ S, ∀ε > 0, ∃δ > 0 : ∀w ∈ D, |z - w| < δ ⇒ |f(z) - f(w)| < ε
Nótese que, de acuerdo a esta definición, fijados z y ε, es posible obtener un δ que podría variar si cambia ε o cambia z.
Definición: Sean f : D ⊂ ℂ ⟶ ℂ, y S ⊂ D. Se dice que f es uniformemente continua en S si
∀ε > 0, ∃δ > 0 : ∀z ∈ S, ∀w ∈ D, |z - w| < δ ⇒ |f(z) - f(w)| < ε
Es decir, en la continuidad uniforme, fijado ε, se obtiene δ que sirve para todo z ∈ S.
Obviamente, toda función uniformemente continua en S es continua en S, pero la recíproca no es cierta en general. Sin embargo, hay un importante caso en que una función continua es uniformemente continua.
Ejercicios propuestos:
Guia de Unidad 2: Funciones Complejas y Unidad 3: Derivación en el Campo Complejo
Ejercicios propuestos:
Guia de Unidad 2: Funciones Complejas y Unidad 3: Derivación en el Campo Complejo


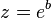
No hay comentarios:
Publicar un comentario