Fórmula integral de Cauchy
Esta fórmula, debida a Cauchy, es parte fundamental del Cálculo Integral de variable compleja.
Definición
Enunciado 1
Sea f(z) una función analítica en un dominio simplemente conexo D. Entonces para cualquier punto z0 contenido en el interior de D y para cualquier camino C cerrado simple que contenga al punto se tiene
k = n + 1. ( donde k es el orden del polo de valor z = z0)
donde la integración está tomada en sentido antihorario.
Enunciado 2
Sea f una función holomorfa (función analítica) sobre γ, γ un camino (una curva diferenciable con continuidad a trozos) cerrado y z0 ∉ γ
Siendo z0 un punto, Iγ(z0) el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
Teorema de Morera.
El presente tema estará dedicado al estudio de (la) conveniente convergencia de sucesiones de funciones holomorfas en un abierto dado ∑n≥0 (z – a)n La convergencia puntual será una noción muy débil. Por otro lado, de una serie de potencias sólo cabe esperar, en general, convergencia uniforme cuando an = 0 a partir de un momento, en adelante la convergencia adecuada, y que da nombre a este tema, nos viene dada por el comportamiento de las series de potencias en su disco de convergencia. Un paso más, será el logro de una topología en el espacio de las funciones holomorfas cuya convergencia sea la uniforme sobre compactos; veremos que tal topología es metrizable, pero no proviene de ninguna norma. El resultado central de este tema es, sin duda, el teorema de Weierstrass. Para su prueba contaremos con una inestimable ayuda: el teorema de Morera, el cual es, realmente, un recíproco del teorema de Cauchy-Goursat.
Notación:
Escribiremos
cuando queramos expresar que una sucesión (fn) converge uniformemente sobre los compactos de cierto abierto a una función f.
Teorema (de Morera). Sea f : Ω → C una función continua sobre un abierto del plano. Supongamos que
para todo triángulo ∆ ⊂ Ω. Entonces f ∈ H(Ω).
Demostración. Para a ∈ Ω, consideremos un r > 0 tal que D(a,r) ⊂ Ω Para cada z ∈ D(a,r) definimos
Por ser los discos abiertos: si b ∈ D(a,r), existirá ρ>0, tal que D(b,ρ) ⊂ D(a,r); y por ser convexos, si z ∈ D(b,ρ), entonces ∆:=∆(a, b, z) ⊂ D(a,r)⊂ Ω Asi, por el teorema de Cauchy-Goursat, tenemos que
de donde, aplicando el lema de construcción de primitivas, por la arbitrariedad de z en D(b,ρ) se tiene que F es una primitiva para f en D(a,r).
En consecuencia, f ∈ H(D(a, r) ). Pero, igualmente, a también es arbitrario en el abierto �� luego f ∈ H(Ω).
Teorema de Liouville
Delainvarianciadelvolumenenelespaciodelasfasessededuceelteoremab´asico de la Mecánica estadística, el teorema de Liouville.
Imaginemos un número muy grande de réplicas absolutamente idénticas de un dado sistema, que difieren unas de otras solamente en sus estados iniciales
Todas estas réplicas forman lo que se denomina un ensemble estadístico del sistema. Un ejemplo de ensemble lo constituyen las moléculas de un gas en un dado volumen.
A cada elemento de volumen ∆V del espacio de las fases podemos asignarle un dado número de réplicas ∆N. Al evolucionar el sistema, estas réplicas pasarán a ocupar un nuevo volumen que, por la demostración de la sección anterior, no varía. En otras palabras, la densidad del ensemble
permanece constante. O sea dρ / dt = 0
Con esto hemos demostrado el siguiente teorema.
La densidad de un ensemble estadístico es una integral de movimiento o en forma expandida
donde hago la presentación formal de un operador que en diferentes formas nos acompañara a lo largo de toda la carrera, el corchete de Poisson
Teorema fundamental del álgebra
El teorema fundamental del álgebra establece lo siguiente:
Todo polinomio de grado n, con coeficientes complejos, tiene exactamente n raíces, no forzosamente distintas, es decir contadas con su orden de multiplicidad.
Por ejemplo, el polinomio real (y por lo tanto también complejo):
x3 − 2x2 − 4x + 8 = (x − 2)2(x + 2)
Tiene 2 como raíz doble, y -2 como raíz simple, lo que da en total tres raíces.
En otras palabras, todo polinomio:
P(x) = anxn + an-1xn-1 + … + a1x + a0
se puede factorizar completamente, así:
an· (x – z0) · (x – z0) ·…· (x – zn)
con los zi complejos, y an ≠ 0.
Teorema del valor medio de Gauss
Sea f(z) una función analítica en un dominio simplemente conexo D. Sea z = z0 + reiθ, donde 0 ≤ r ≤ r0 y 0 ≤ θ ≤ 2π, un circulo de centro en z0 y radio r0 > 0 perteneciente a D. Entonces,
La expresión de la derecha de la ecuación es la media aritmética o valor medio de f(z) a lo largo de la circunferencia del circulo. El teorema del valor medio de Gauss puede usarse para demostrar importantes propiedades de las funciones analíticas:
— teorema del modulo máximo:
Si f(z) es analítica y no constante en el interior de una región, entonces |f(z)| no tiene máximo en esa región.
— Principio del modulo mínimo:
Si f(z) es analítica no nula y no constante en el interior de una región, entonces |f(z)| no tiene mínimo en esa región.
Formula integral de poisson para circulo
Si f es una función analítica en un dominio que contiene al círculo unidad, entonces la Fórmula Integral de Cauchy nos dice que para un punto de dicho círculo z0 ≠ 0 se tiene.
Sea r = |z0| y consideremos el punto
exterior al círculo unidad. El Teorema de la Integral de Cauchy nos dice que
Restando estas expresiones obtenemos
Ahora parametrizamos C mediante z(t) = ejt con 0 ≤ t ≤ 2π, con lo que obtenemos
Ahora, escribiendo z0 = rejθ, z1 = r-1 rejθ y operando, nos queda
fórmula que también es válida para r = 0 (que es el Teorema del Valor Medio de Gauss). Finalmente, separando en partes real e imaginaria obtenemos, como hemos dicho antes, la Fórmula Integral de Poisson para funciones armónicas que vimos antes
El problema de Dirichlet en el semiplano superior.
La función bilineal ω=(j-z)/(j+z) transforma el eje real Lm (z) = 0 en la circunferencia unidad |ω| = 1 de forma que el semiplano superior del plano z se transforma de manera conforme en el interior del círculo unidad del plano ω. Si queremos hallar una función u(x, y) armónica en el semiplano superior a partir de sus valores u(x, 0) en el eje real, podemos usar la transformación bilineal para llevarnos el problema al círculo unidad, usar ahí la fórmula de Poisson y deshacer la transformación. Haciendo las operaciones con cuidado se obtiene la solución, que además es acotada,

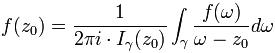


















No hay comentarios:
Publicar un comentario